Calculation of pi, π
1. Adding the length of sides of inscribed polygons which their sides double in number - because they fold (not completely) and the folded angle touches the circumference, see below: green to red line - at every new calculation. Circumference=2πr, r=1 => π=1/2(Circumference).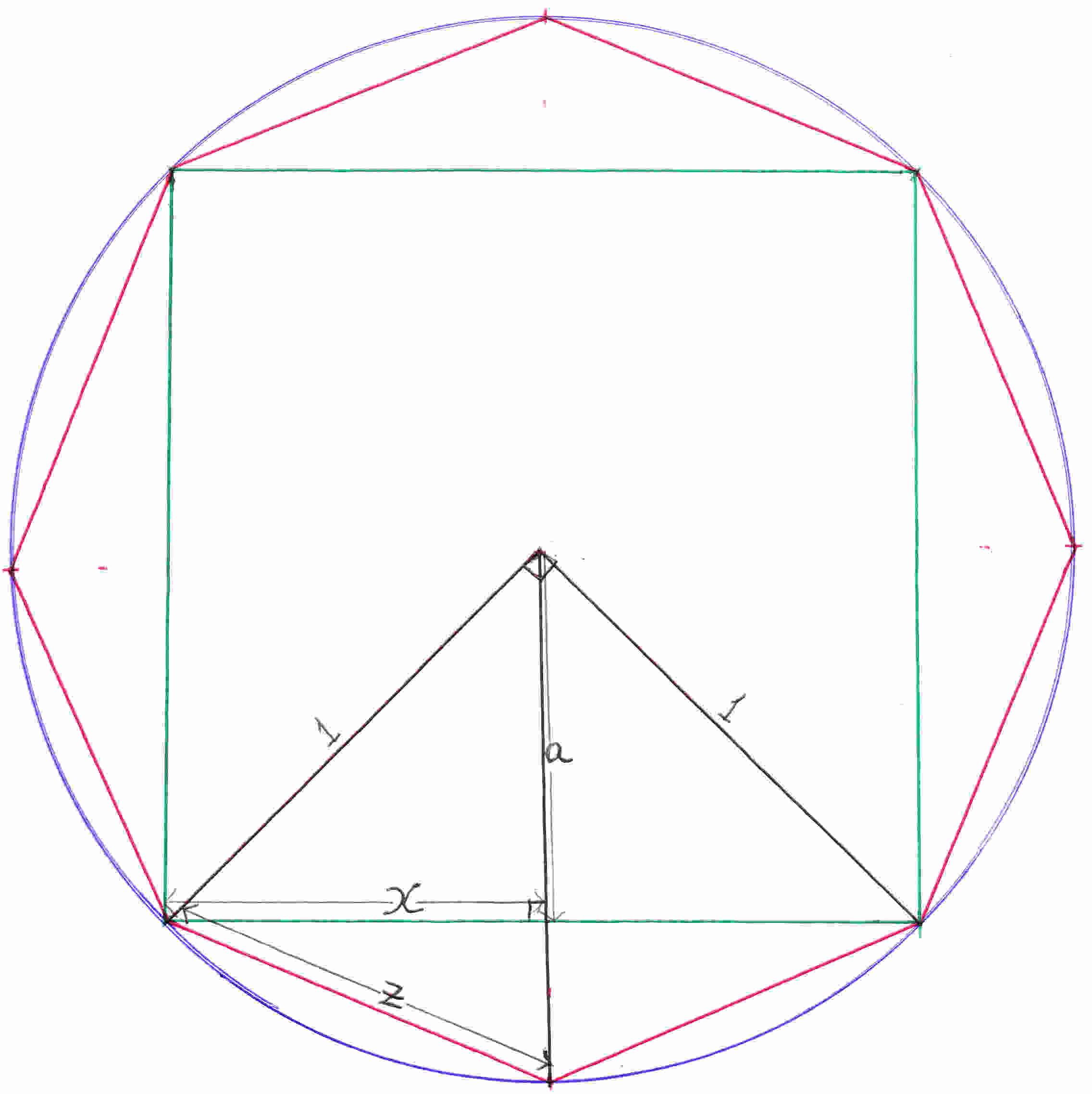
a2=1-x2
∴a=√ 1 - x2
From the small triangle underneath where ƶ is the hypotenuse:
ƶ2=(1-a)2 +x2
ƶ2=1 -2a +a2 +x2
Substituting a with x:
ƶ2=1 -2√ 1 - x2 +1 -x2 +x2
ƶ2=2 -2√ 1 - x2
ƶ=√ 2 -2√ 1 - x2
The value of x which is half the hypotenuse of the right angle(center) triangle is √ 2 /2.
Then, where x which is half the side of the green square we substitute with ƶ/2 and the result we substitute it again. This is done continuously calculating the half side of polygons. In the following estimation of π at small values of the half side of the polygon the calculation is not that accurate. A supercomputer can do it.
Circumference (perimeter) of circle=2πr
Perimeter of polygon with infinite sides and radius 1 meter=2π
Number of sides of polygon ✕ length of one side with half diagonal(radius=1m)=2π
Number of sides of polygon ✕ length of half side of polygon with radius 1m=π:
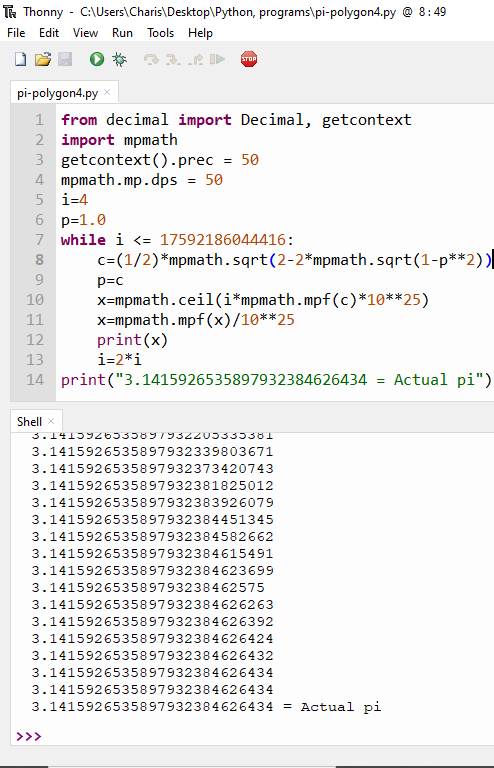
From the above we multiply the figure in the first column below by that in the second column to find pi.
The number of sides of the polygon is 2 to the power of an integer because at every new additional calculation the number of sides double as it has been previously explained.
Enter an integer in the box below:
Using Python
x: length of the side of the said polygon
n→∞, x→0
2. Adding the length of the segments with the width you input.
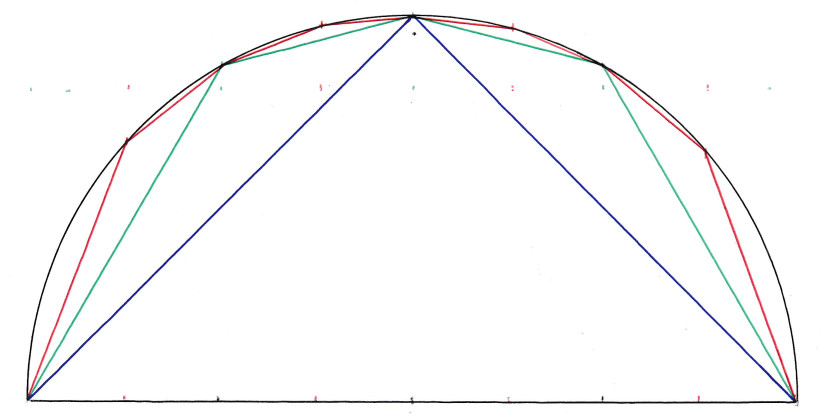
From the figure above when the width is 1 is shown by the blue line. When the width is 0.5 green line. Width 0.25 red line. When the width is reduced, you will input it, the line resembles the semicircle. The smallest the width the more accurate the circle and the calculation of pi will be. We start from the left -1. Then we add 0.1 therefore x=-0.9 we find y which is y2=1-x2 (equation of circle with radius 1). We know x and y: x1=-1, y1=0, x2=-0.9, y2=√ 1 - (-0.9)2 =0.436. We know the coordinates of two points we find the distance between them by d2=(x2-x1)2+(y2-y1)2. Similarly we find the distance between all points and add them up. This is the circumference of the semicircle above (radius=1)=pi.
You have the opportunity to input the width. The smaller the more accurate pi will be but it takes more time for the computer to calculate it. For very small values you will have to wait for some time, press the button once, that is why values less than 0.0000001 are not accepted. Values that divide 2 perfectly give a more accurate pi because the range is 2, from -1 to 1. You can play as many times as you like. There is no limit.
π=3.1415926535898
3. Adding the area of the segments with the width you input.
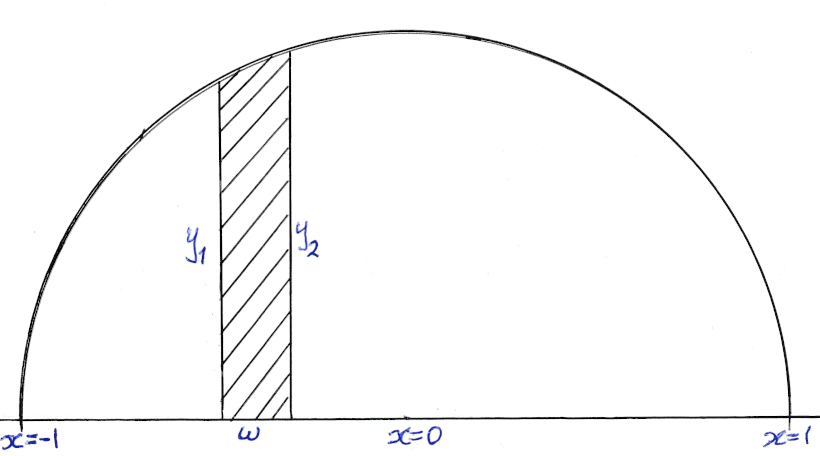
The semi-circle is divided into segments like the one above (shaded area) with width w. The one side of the segment is y1=√ 1 - x2 (equation of circle with radius=1) the other side of the segment is y2=√ 1 - (x+w)2 . The area of the segment(trapezium) =1/2(y1+y2)w. We add all segments from x=-1 to x=1 thus we find the area of the semi-circle=1/2πr2, r=1 => area=π/2 =>π=2area.
π=3.1415926535898

Go to the Home page.
Go to the Early Jewish Writings.